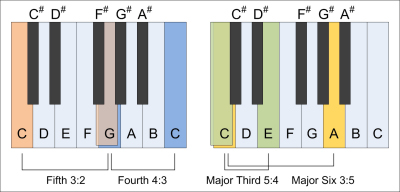
The following relations in frequency or in the length of a vibrating string are the harmonic tones, the consonant intervals in music:
| 1 : 1 | = | Unison |
| 2 : 1 | = | Octave |
| 3 : 2 | = | Fifth |
| 4 : 3 | = | Fourth |
| 5 : 4 | = | Major Third |
| 3 : 5 | = | Major Six |
To bring all these intervals together on one basis the number '12' is the most fitting one. This explains why todays music is built by 12 'semi-tones'. All the rations above can be expressed in a ratio on the basis of twelve:
| 12 : 12 | = | Unison |
| 12 : 6 | = | Octave |
| 12 : 8 | = | Fifth |
| 12 : 9 | = | Fourth |
| 12 : 9.6 | = | Major Third |
| 12 : 20 | = | Major Six |
This relationship was fist introduces by Pythagoras two and a half thousand years ago.
The most consonant interval is the octave with a frequency ratio of 2:1. The next most consonant intervals are the fifth and the fourth with a frequency ratio of 3:2 and 4:3.

A vibrating string or any other vibrating body has also overtones as integer multiples of its fundamental frequency.
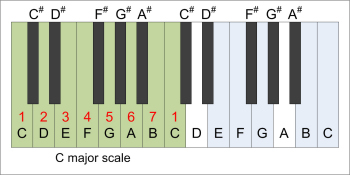 | 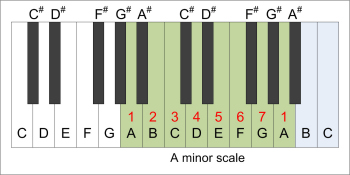 |
| C major scale | parallel A minor scale |
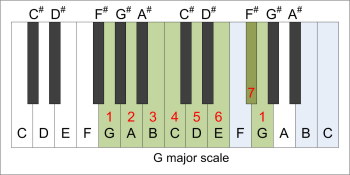 | 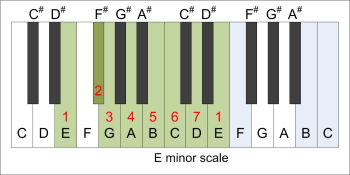 |
| G major scale | parallel E minor scale |
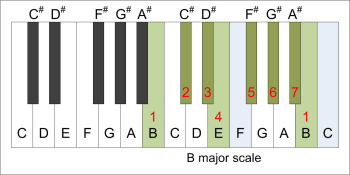 | 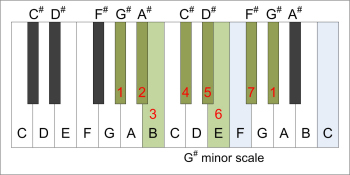 |
| B major scale | parallel G# minor scale |
| C Major | Interval | half steps | scale degrees |
| C | unison | 0 | tonic |
| D | major 2nd | 2 | supertonic |
| E | major 3rd | 4 | mediant |
| F | perfect 4th | 5 | subdominant |
| G | perfect 5th | 7 | dominant |
| A | major 6th | 9 | submediant |
| B | major 7th | 11 | leading tone |
| C | octave | 12 | octave |
An interval is the distance between two notes. Interval values can be referred to as M (Major), m (minor), A (Augmented), or d (diminished).
The perfect intervals are: unison, perfect 4th, perfect 5th und octave,
the major intervals are: major 2nd, major 3rd, major 6th, major 7th,
the minor intervals are: minor 2nd, minor 3rd, minor 6th, minor 7th.
| Half-Steps | Notes | Interval (English) | Interval (German) | |
| 0 | C | unison | Prime | |
| 1 | C# | Db | minor 2nd | Kleine Sekunde |
| 2 | D | major 2nd | (Grosse) Sekunde | |
| 3 | D# | Eb | minor 3rd | Kleine/Moll-Terz |
| 4 | E | major 3rd | Grosse/Dur-Terz | |
| 5 | F | perfect 4th | (Reine) Quarte | |
| 6 | F# | Gb | diminished 5th | Verminderte Quinte |
| 7 | G | perfect 5th | Quinte | |
| 8 | G# | Ab | augmented 5th or minor 6th | Übermässige Quinte, kleine Sexte |
| 9 | A | major 6th | Sexte | |
| 10 | A# | Bb (Hb) | minor 7th | Kleine Septime |
| 11 | B (H) | major 7th | Septime | |
| 12 | c | octave | Oktave | |
| 13 | c# | db | flat 9th | Kleine None |
| 14 | d | 9th | None | |
| 15 | d# | eb | sharp 9th == minor 3rd (one octave) | Kleine Dezime |
| 16 | e | major 10th == major 3rd (one octave) | Dezime | |
| 17 | f | 11th | Undezime | |
| 18 | f# | gb | augmented 11th | Überm. Undezime |
| 19 | g | perfect 12th == perfect 5th (one octave) | Duodezime | |
| 20 | g# | ab | flat 13th | Verminderte Tredezime |
| 21 | a | 13th | Tredezime | |
The so called perfect intervals are: unison, perfect 4th, perfect 5th und octave,
the major intervals are: major 2nd, major 3rd, major 6th, major 7th,
the minor intervals are: minor 2nd, minor 3rd, minor 6th, minor 7th.
In the 19th century the British Alexander John Ellis introduced the Cent as a measurement for a tonal difference between two tones.
Every of the 12 half-step tones of one octave is separated by 100 logarithmic steps, the Cent.
One full-step tone equals 200 Cent and one octave equals 1200 Cent.
The term TONE refers to an interval, the term NOTE refers to a certain pitch.
Chords are three or more pitches played simultaneously. The basic musical chords are the major chord and the minor chord.
Major chord: prime, major 3rd, minor 3rd, minor accord: prime minor 3rd, major 3rd.
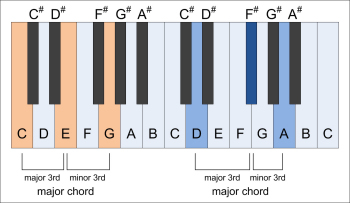 | 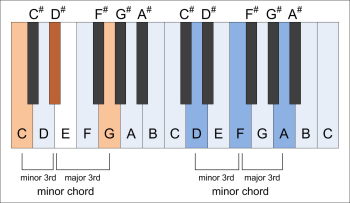 |
| two major chords | two minor chords |